VECTORES CONCURRENTES

Un sistema de vectores es concurrentes cuando la dirección de los vectores se cruza en algún punto.

El punto de cruce es el punto de aplicaron de los vectores.

Se les llama angulares porque forman angulares porque forman  un ángulo entre ellos

COMPONENTES DE UN VECTOR

componentes de un vector

En un sistema coordenado de dos dimensiones, cualquier vector puede separarse en el componente x y el componente y.

Por

ejemplo, en la figura siguiente mostrada, el vector  se separa en dos componentes, vx

y vy .

Digamos que el ángulo entre el vector y su componente x es θ.

Las relaciones trigonométricas dan la relación entre la magnitud del vector y los componentes del vector.

vx = v cos θ

vy = v sin θ

Usando el Teorema de Pitágoras en el triángulo rectángulo con longitudes vx y vy:

Aquí,

los números mostrados son las magnitudes de los vectores.

Caso 1: Dados los componentes de un vector, encuentre la magnitud y la dirección del vector.

Use las fórmulas siguientes en este caso.

La magnitud del vector es  .

Para encontrar la dirección del vector, resuelva  for θ.

Caso 2: Dada la magnitud y la dirección de un vector, encuentre los componentes del vector.

Use las fórmulas siguientes en este caso.

vx = v cos θ

vy = v sin θ

VECTORES DE POsicion

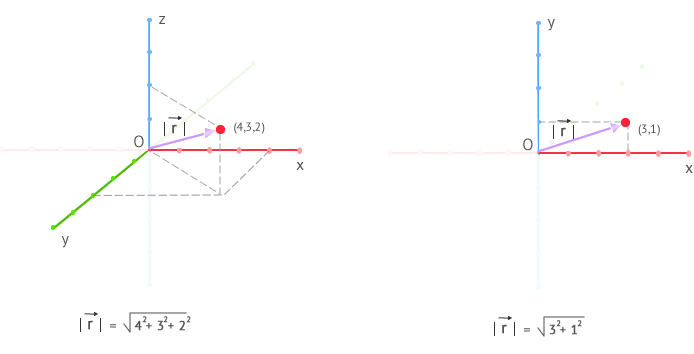
En Física, la posición, vector de posición ó vector posición de un cuerpo respecto a un sistema de referencia se define como el vector que une el lugar ocupado por el cuerpo con el origen del sistema de referencia. Su expresión, en coordenadas cartesianas:

r⃗ =xi⃗ +yj⃗ +zk⃗ 

donde:

r⃗  : es el vector de posición

x, y, z : Son las coordenadas del vector de posición

i⃗ ,j⃗ ,k⃗  :Son los vectores unitarios en las direcciones de los ejes OX, OY y OZ respectivamente