VIDEO

VECTORES CONCURRENTES

Un sistema de vectores es concurrentes cuando la dirección de los vectores se cruza en algún punto.

El punto de cruce es el punto de aplicaron de los vectores.

Se les llama angulares porque forman angulares porque forman  un ángulo entre ellos

COMPONENTES DE UN VECTOR

componentes de un vector

En un sistema coordenado de dos dimensiones, cualquier vector puede separarse en el componente x y el componente y.

Por

ejemplo, en la figura siguiente mostrada, el vector  se separa en dos componentes, vx

y vy .

Digamos que el ángulo entre el vector y su componente x es θ.

Las relaciones trigonométricas dan la relación entre la magnitud del vector y los componentes del vector.

vx = v cos θ

vy = v sin θ

Usando el Teorema de Pitágoras en el triángulo rectángulo con longitudes vx y vy:

Aquí,

los números mostrados son las magnitudes de los vectores.

Caso 1: Dados los componentes de un vector, encuentre la magnitud y la dirección del vector.

Use las fórmulas siguientes en este caso.

La magnitud del vector es  .

Para encontrar la dirección del vector, resuelva  for θ.

Caso 2: Dada la magnitud y la dirección de un vector, encuentre los componentes del vector.

Use las fórmulas siguientes en este caso.

vx = v cos θ

vy = v sin θ

VECTORES DE POsicion

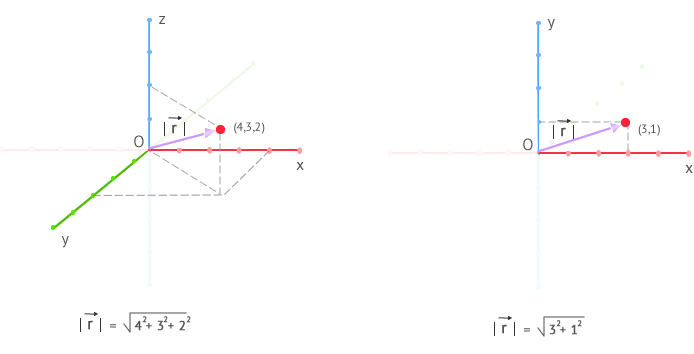
En Física, la posición, vector de posición ó vector posición de un cuerpo respecto a un sistema de referencia se define como el vector que une el lugar ocupado por el cuerpo con el origen del sistema de referencia. Su expresión, en coordenadas cartesianas:

r⃗ =xi⃗ +yj⃗ +zk⃗ 

donde:

r⃗  : es el vector de posición

x, y, z : Son las coordenadas del vector de posición

i⃗ ,j⃗ ,k⃗  :Son los vectores unitarios en las direcciones de los ejes OX, OY y OZ respectivamente

Regla del paralelogramo

Se toman como representantes dos vectores con el origen en común, se trazan rectas paralelas o los vectores obteniéndose un paralelogramo cuya diagonal coincide con la suma de los vectores

Para sumar dos vectores se suman sus respectivos componentes.

 En un paralelogramo cualquiera la suma de los cuadrados de las longitudes de las diagonales es igual al doble de la suma de los cuadrados de las longitudes de dos lados contiguos.

MULTIPLICACIÓN DE VECTORES 

Un vector se define como una cantidad con dirección y magnitud. Dos vectores pueden multiplicarse para presentar un producto escalar a través de una fórmula de producto en punto. El producto en punto se usa para determinar si dos vectores son perpendiculares uno con otro. Por otro lado, dos vectores pueden producir un tercero, donde el vector resultante utiliza la fórmula de producto cruzado. El producto cruzado arregla los componentes del vector en una matriz de líneas y columnas. Permite al estudiante determinar la magnitud de las fuerzas resultantes y la dirección con poco esfuerzo.

PRODUCTO DE UN ESCALAR POR UN VECTOR 

El producto de un escalar por un vector da por resultado otro vector, con la misma dirección que el primero. Al hacer la multiplicación, el escalar cambia el módulo del vector (gráficamente el largo) y en caso de ser negativo cambia también el sentido. La dirección del vector resultado es siempre la misma que la del vector original.

Matemáticamente se realiza multiplicando al escalar por cada una de las componentes del vector.

Si por ejemplo el vector V tiene 2 coordenadas:

V = (x, y)

k V =  k (x, y) = (kx, ky)

Ejemplo:

V = (2,1)

k = 2

k V = 2 (2, 1) = (4, 2)

EJEMPLO 

V= (2, 2)

k = -1

k V = -1 (2, 2) =  (-2, -2)

si  los vectores son de mas de dos coordenadas se realiza lo mismo por cada una de ellas 

tomado de: www.wikipedia.com

www.wikipedia.com

Vectores LINEAL MENTE dependientes 

Varios vectores libres del plano se dice que son lineal mente dependientes si hay una combinación lineal de ellos que es igual al vector cero, sin que sean cero todos los coeficientes de la combinación lineal.

PROPIEDADES

 1.:si varios vectores son lineal mente dependientes, entonces al menos uno de ellos se puede expresar como combinación lineal de los demás.

2 Dos vectores del plano son lineal mente dependientes si, y sólo si, son paralelos.

3 Dos vectores libres del plano u = (u1, u2) y v = (v1, v2) son lineal mente dependientes si sus componentes son proporcionales

Vectores LINEAL MENTE independientes

Varios vectores libres son lineal mente independientes si ninguno de ellos puede ser escrito con una combinación lineal de los restantes.

Vectores lineal mente dependientes

a1 = a2 = ··· = an = 0

Los vectores lineal mente independientes tienen distinta dirección y sus componentes no son proporcionales.

Ejemplo:

Determinar si son lineal mente dependientes o independientes los vectores.

u = (3, 1) y v = (2, 3)

Son lineal mente independientes

Suma de vectores

 Suma de Componentes

La suma gráfica de vectores con regla y transportador a veces no tiene la exactitud suficiente y no es útil cuando los vectores están en tres dimensiones.

Sabemos, de la suma de vectores, que todo vector puede descomponerse como la suma de otros dos vectores, llamados las componentes vectoriales del vector original. Para sumarlos, lo usual es escoger las componentes sumando a lo largo de dos direcciones perpendiculares entre sí.

Ejemplo Suma Vectores: suponga un vector V cualquiera

Trazamos ejes coordenados x y con origen en la cola del vector V. Se trazan perpendiculares desde la punta del vector V a los ejes x y y determinándose sobre el eje x la componente vectorial Vx y sobre el eje y la componente vectorial V

tomado de : www.wikipedia.com

EJEMPLOS DE CALCULO VECTORIAL

EJEMPLO: Dado el vector V de componentes (3,-5), normalizarlo.

Normalizar un vector consiste en ponerlo en función de sus vectores

unitarios, es decir, manifestar las componentes del vector V en función

de sus componentes según los ejes de coordenadas.

 V = 3 . i + (-5) . j ; V = 3 . i - 5 . j

CLASES DE VECTORES

Existen 6 clases de vectores que son:

                   Vectores equipolentes

Dos vectores son equipolentes cuando tienen igual módulo, dirección y sentido.

Vectores libres

El conjunto de todos los vectores equipolentes entre sí se llama vector libre. Es decir los vectores libres tienen el mismo modulo, dirección y sentido.

Vectores fijos

Un vector fijo es un representante del vector libre. Es decir, los vectores fijos tienen el mismo módulo, dirección, sentido y origen.

Vectores ligados

Los vectores ligados son vectores equipolentes que actúan en la misma recta. Es decir, los vectores fijos tienen el mismo módulo, dirección, sentido y se encuentran en la misma recta.

Vectores opuestos

Los vectores opuestos tienen el mismo módulo, dirección, y distinto sentido.

Vectores unitarios

Los vectores unitarios tienen de módulo, la unidad. Para obtener un vector unitario, de la misma dirección y sentido que el vector dado se divide éste por su módulo

Vectores unitarios

Los vectores unitarios tienen de módulo, la unidad. Para obtener un vector unitario, de la misma dirección y sentido que el vector dado se divide éste por su módulo.

tomado de: https://es.wikipedia.org/wiki/Vector

https://es.wikipedia.org/wiki/vector unitario

https://es.wikipedia.org/wiki/C%C3%A1lculo_vectorial

QUE ES UN VECTOR 

Vector es un término que deriva de un vocablo latino y que significa “que conduce”. Un vector es un agente que transporte algo de un lugar a otro. Su significado, de todas formas, varía de acuerdo al contexto.

Vector

Un vector puede utilizarse para representar una magnitud física, quedando definido por un módulo y una dirección u orientación. Su expresión geométrica consiste en segmentos de recta dirigidos hacia un cierto lado, asemejándose a una flecha. La velocidad y la fuerza son dos ejemplos de magnitudes vectoriales.

UNA DIRECCIÓN

La dirección de un vector es la dirección de la recta que contiene al vector o de cualquier recta paralela a ella.

UN SENTIDO

El sentido del vector AB es el que va desde el origen A al extremo B.

UN MODULO 

El módulo del vector  es la longitud del segmento AB, se representa por !AB! 

El modulo de un vector es un numero siempre positivo o cero 

CALCULO VECTORIAL

El cálculo vectorial o análisis vectorial es un campo de las matemáticas referidas al análisis real multivariable de vectores en 2 o más dimensiones. Es un enfoque de la geometría diferencial como conjunto de fórmulas y técnicas para solucionar problemas muy útiles para la ingeniería y la física.

Consideramos los campos vectoriales, que asocian un vector a cada punto en el espacio, y campos escalares, que asocian un escalar a cada punto en el espacio. Por ejemplo, la temperatura de una piscina es un campo escalar: a cada punto asociamos un valor escalar de temperatura. El flujo del agua en la misma piscina es un campo vectorial: a cada punto asociamos un vector de velocidad.

Cuatro operaciones son importantes en el cálculo vectorial que son:

Gradiente: mide la tasa y la dirección del cambio en un campo escalar; el gradiente de un campo escalar es un campo vectorial.

Rotor o rotacional: mide la tendencia de un campo vectorial a rotar alrededor de un punto; el rotor de un campo vectorial es otro campo vectorial.

Divergencia: mide la tendencia de un campo vectorial a originarse o converger hacia ciertos puntos; la divergencia de un campo vectorial es un campo escalar.

Laplaciano: relaciona el "promedio" de una propiedad en un punto del espacio con otra magnitud, es un operador diferencial de segundo orden.

La mayoría de los resultados analíticos se entienden más fácilmente usando la maquinaria de la geometría diferencial, de la cual el cálculo vectorial forma un subconjunto.

webgrafia:

http://definicion.de/vector/
https://es.wikipedia.org/wiki/Vector
https://es.wikipedia.org/wiki/C%C3%A1lculo_vectorial